SOLUTION: the mean of two positive numbers is equal to their difference. Three times this difference is equal to twice the value of the larger of the two numbers. What can you conclude about

Algebra ->  Systems-of-equations -> SOLUTION: the mean of two positive numbers is equal to their difference. Three times this difference is equal to twice the value of the larger of the two numbers. What can you conclude about      Log On


   

Question 1133856: the mean of two positive numbers is equal to their difference. Three times this difference is equal to twice the value of the larger of the two numbers. What can you conclude about these two numbers?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39621) About Me  (Show Source):
Answer by ikleyn(52818) About Me  (Show Source):
You can put this solution on YOUR website!
.

x and y;
x%3Cy


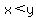Description turned into equations:  


x+y=2(y-x),     (1) 
3(y-x)=2y       (2)


From equation (1)

3x = y          (3)


From equation (2)

y = 3x          (4)


Equations (3) and (4) are identical. 

It means that lesser number, x, may have any value, and greater number, y, must be 3 times the smaller.


ANSWER.  Lesser number, x, may have any positive real value, and greater number, y, must be 3 times the smaller.