SOLUTION: Each side of a regular octagon is y cm long find the distance in cm between any two parallel sides of this octagon Please try to solve without sin cos tan please

Algebra ->  Triangles -> SOLUTION: Each side of a regular octagon is y cm long find the distance in cm between any two parallel sides of this octagon Please try to solve without sin cos tan please      Log On


   

Question 1133757: Each side of a regular octagon is y cm long find the distance in cm between any two parallel sides of this octagon
Please try to solve without sin cos tan please
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

Image and video hosting by TinyPic

in your case a=y
apothem is sqrt%282%29y%2F2%2By%2F2=%28sqrt%282%29y%2By%29%2F2=y%28sqrt%282%29%2B1%29%2F2

distance between two parallel sides is twice the length of apothem
distance=2%2Ay%28sqrt%282%29%2B1%29%2F2
distance=cross%282%29%2Ay%28sqrt%282%29%2B1%29%2Fcross%282%29
distance=y%28sqrt%282%29%2B1%29

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Each side of a regular octagon is y cm long find the distance in cm between any two parallel sides of this octagon
Please try to solve without sin cos tan please
This is a REGULAR OCTAGON so all sides and all angles are congruent.

The distance between 2 parallel sides of an octagon is twice the measure of its apothem.

The APOTHEM is the ALTITUDE drawn from the APEX of the octagon to each base of the 8 isosceles triangles in the octagon.

The APOTHEM is also opposite the 60o angle of any of the 2 right triangles, formed when the altitude is drawn, and represents the longer leg too

The length of the APOTHEM/ALTITUDE/LONGER LEG (opposite the 60o angle) is the length of the SHORTER Leg * 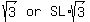matrix%281%2C3%2C+sqrt%283%29%2C+or%2C+SL+%2A+sqrt%283%29%29

Since the length of one of the sides is y, the shorter leg (SL) of any one of the 2 right triangles, in this case, is y%2F2,

so the length of the APOTHEM is: matrix%281%2C3%2C+%28y%2F2%29+%2A+sqrt%283%29%2C+%22=%22%2C+y%2Asqrt%283%29%2F2%29. 

Now, with the distance being twice the length of the APOTHEM, we get: