Question 1133747: Can you please solve this?
On the first part of a 276-mile trip, a salesperson averaged 63 miles per hour. The salesperson averaged only 54 miles per hour on the last part of the trip because of an increased volume of traffic.
(a) Write the total time t for the trip as a function of the distance x traveled at an average speed of 63 miles per hour.
t(x) =
(b) Use a graphing utility to graph the time function. What is the domain of the function? (Enter your answer using interval notation.)
(c) Approximate the number of miles traveled at 63 miles per hour when the total time is 4 hours and 45 minutes.
x = mi
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let T1 = the time traveled at 63 miles per hour.
let T2 = the time traveled at 54 miles per hour.
since the total distance traveled is 276 miles, your first equation will be:
63 * T1 + 54 * T2 = 276
if you let T = the total time, then:
T = T1 + T2
you are given that the distance traveled at 63 miles per hour is x miles.
this means that 63 * T1 = x
solve for T1 to get T1 = x/63
your original equation is 63 * T1 + 54 * T2 = 276
since 63 * T1 = x, this equation becomes x + 54 * T2 = 276 after you replace 63 * T1 with x.
subtract 54 from both sides of this equation to get 54 * T2 = 276 - x
divide both sides of this equation by 54 to get T2 = (276 - x) / 54
you now have:
T1 = x / 63
T2 = (276 - x) / 54
since T = T1 + T2, then T = x / 63 + (276 - x) / 54
let t(x) = T and you get t(x) = x/63 + (276 - x) / 54
the domain of this function will be 0 <= x <= 276
x cannot be less than 0 because then the distance traveled at 63 miles per hour will be negative.
x cannot be greater than 276 because then the distance traveled at 54 miles per hour would be negative.
the range of this function will be the value ot t(x) from when x = 0 to x = 276.
when x = 0, t(x) = 0/63 + 276/54 = 5.11111..... = 5.111 rounded to 3 decimal digits.
when x = 276, t(x) = 276/63 + 0/54 = 4.380952381 = 4.381 rounded to 3 decimal digits.
when t(x) = 4 hours and 45 minutes, you get t(x) = 4.75 hours because 45 minutes is equal to .75 hours.
since t(x) = x/63 + (276-x)/54, then the equation becomes 4.75 = x/63 + (276-x)/54.
the graph of the equation replaces t(x) with y to get y = x/63 + (276-x)/54.
t(x) = 4.75 means that y = 4.75 on the graph because y represents t(x) on the graph.
in the graph, i set y = 4.75.
the intersection of that value of y with the equation of y = x/63 + (276-x)/54 occurs when x = 136.5.
that means that the distance traveled at 63 miles per hour was 136.5 miles.
answer to (a) is t(x) = x/63 + (276-x)/54
answer to (b) is the domain of the function is 0 <= x <= 276.
answer to (c) is the number of miles traveled at 63 miles per hour is 136.5.
those are your solutions.
this is what the graph looks like.
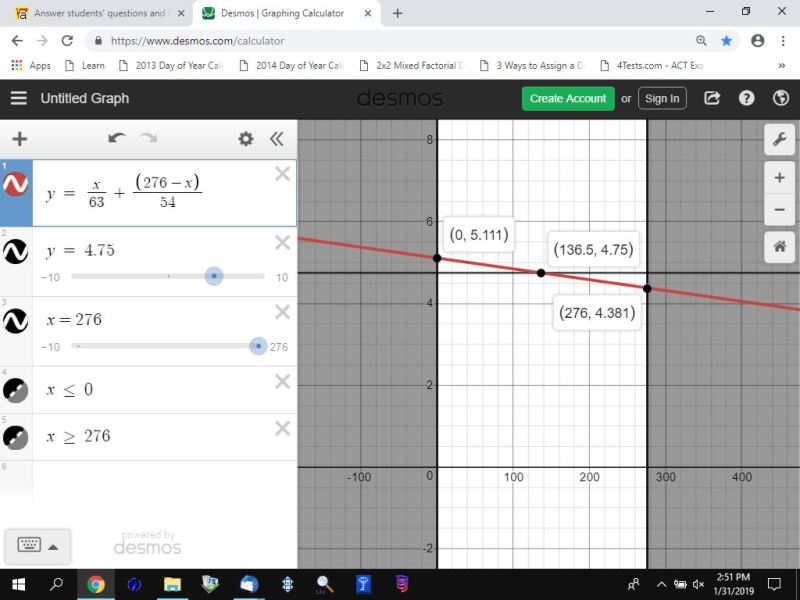
since the number of miles traveled at 63 miles per hour is 136.5, then the number of miles traveled at 54 miles per hour is 276 - 136.5 = 139.5.
you can use this information to solve for the time traveled at 63 miles per hour and the time traveled at 54 miles per hour.
your original equation is 63 * T1 + 54 * T2 = 276
the distance traveled at 63 miles per hour is 136.5 miles.
the time traveled at 63 miles per hour is therefore 136.5/63 = 2.1666666..... hours.
the distance traveled at 54 miles per hour is 139.5 miles.
the time traveled at 54 miles per hour is therefore 139.5/54 = 2.5833333..... hours.
this makes 63 * T1 + 54 * T2 = 276 becomes 63 * 2.16666.... + 54 * 2.583333.... = 276 which becomes 136.5 + 139.5 = 276 which is true.
the solution shown above for (a) and (b) and (c) checks out ok.
|
|
|