|
Question 113366: Find three positive consecutive even integers such that the product of the first and second is 8 more than 38 times the third.
Found 2 solutions by checkley71, solver91311:
Answer by checkley71(8403)   (Show Source):
You can put this solution on YOUR website! X, X+2, X+4 ARE THE 3 POSITIVE CONSECUTIVE INTEGERS.
X(X+2)=8+38(X+4)
X^2+2X=8+38X+152
X^2+2X-38X-8-152=0
X^2-36X-160=0
(X-40)(X+4)=0
X-40=0
X=40 ANSWER FOR THE FIRST INTEGER.
40+2=42 FOR THE SECOND INTEGER.
40+4=44 FOR THE THIRD INTEGER.
PROOF
40*42=8+38*44
1680=8+1672
1680=1680
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! If the first integer is x, the next even integer is x + 2, and the next one after that is x + 4.
The product of the first and second is simply x(x + 2), and 38 times the third is 38(x + 4). Now we can translate the problem.
The product of the first and second (x(x + 2)) is (=) 8 more (+) than 38 times the third (38(x + 4)).
 . Using the distributive property and combining terms we get:
If you note that  and  , you can see this quadratic equation is factorable.
 , which is true if and only if
 or  . Therefore,
 or 
However, we can exclude the negative result because the problem asks for three POSITIVE consecutive even integers.
So, the first number is 40, the second is 42, and the third is 44.
Last step: VERY IMPORTANT -- Check your answer.
40 * 42 = 1680
38 * 44 = 1672. Add 8 to that and get 1680. Answer checks.
Hope this helps,
John
P.S. I was looking this over carefully before I sent it and noted that the problem refers to the first, second, and third consecutive positive even integers. Now that strongly implies that the numbers we are looking for are in order as to size, but it doesn't necessarily mean that they are in ASCENDING order. That allows for the possibility that the first number is the largest one, the second one 2 smaller than the first, and the third 2 smaller than that. Given that assumption, the problem works out this way:
First = x
Second = x - 2
Third = x - 4
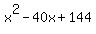
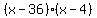
So x = 36, x - 2 = 34, and x - 4 = 32.
36 * 34 = 1224, and (38 * 32) + 8 = 1224, so this checks.
The other root is positive this time, but that would mean that the numbers are 4, 2, and 0. Most authorities agree that zero is neither positive nor negative and therefore doesn't fit the conditions of the problem, so we can again exclude this solution.
The point is, always consider all reasonable possibililties. Ask your instructor to explain, if s/he disagrees with the above analysis, why the first number must be the smallest -- and don't settle for a "because everybody does it that way" sort of answer.
J.
|
|
|
| |
