Question 1133505: A pizza parlor has a choice of
12
toppings for its pizzas. From these
12
toppings, how many different
6
-topping pizzas can be ordered? Assume that the order in which the toppings are listed does not matter.
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Basic combinatorics principles -- permutations and combinations.
If order DID matter, you would have 12 choices for the first topping, then 11 for the second, ..., and 7 for the sixth. The total number of ORDERED sets of toppings (permutations) would be

That number is "12P6", the number of ordered ways (permutations) to choose 6 of 12 things.
In your problem, the order does NOT matter. For that we have the number of combinations of 6 of 12 things, "12C6". To calculate that number, we take the number 12P6, the number of ORDERED ways we could choose 6 of the 12 toppings, and divide it by the number of different ORDERS in which we could have chosen those 6 toppings.
Similar to the reasoning above, we would have 6 choices for the first one we chose, 5 choices for the second, ..., and 1 choice for the sixth. So the number of different ways we could have chosen any particular 6 toppings is 6*5*4*3*2*1 = 720.
Then the number of COMBINATIONS (order doesn't matter) of 6 of 12 toppings is

If you don't have a calculator to do the calculations for you, the calculation to do by hand is
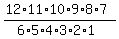
There will always be lots of common factors with which you can simplify the fraction; and if you do the simplification correctly the answer will always be a whole number.
For example, in this calculation 5*2=10 and 4*3=12, so a partially simplified fraction is
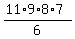
|
|
|