SOLUTION: If {{{(sinA+cosA)/sinAcosA=1/3}}} What is the value of {{{sin^4(A)-cos^4(A)}}}?

Algebra ->  Trigonometry-basics -> SOLUTION: If {{{(sinA+cosA)/sinAcosA=1/3}}} What is the value of {{{sin^4(A)-cos^4(A)}}}?      Log On


   

Question 1133311: If %28sinA%2BcosA%29%2FsinAcosA=1%2F3
What is the value of sin%5E4%28A%29-cos%5E4%28A%29?
Answer by ikleyn(52898) About Me  (Show Source):
You can put this solution on YOUR website!
.

I will solve it in two steps.


Step 1 

For brevity, let's denote x = sin(A)*cos(A).


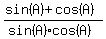%28sin%28A%29+%2B+cos%28A%29%29%2F%28sin%28A%29%2Acos%28A%29%29 = 1%2F3  ====>  square both sides  ====>  


 = %281+%2B+2x%29%2Fx%5E2 = 1%2F9  ====>


9*(1 + 2x) = x%5E2

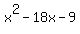x%5E2+-+18x+-+9 = 0

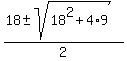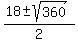x%5B1%2C2%5D = %2818+%2B-+sqrt%2818%5E2+%2B+4%2A9%29%29%2F2 = %2818+%2B-+sqrt%28360%29%29%2F2.


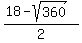Since the modulus of x,  |x|, must be less than 1, only the root   x = %2818+-+sqrt%28360%29%29%2F2  is the solution.


It implies  2x = 2*sin(A)*cos(A) = sin(2A) = 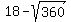18+-+sqrt%28360%29 = 18+-+6%2Asqrt%2810%29.      (1)


Step 2 

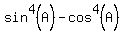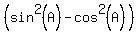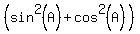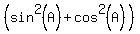sin%5E4%28A%29+-+cos%5E4%28A%29 = %28sin%5E2%28A%29+-+cos%5E2%28A%29%29.%28sin%5E2%28A%29+%2B+cos%5E2%28A%29%29  ====>  replace  %28sin%5E2%28A%29+%2B+cos%5E2%28A%29%29  by 1  ====>


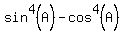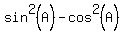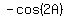sin%5E4%28A%29+-+cos%5E4%28A%29 = sin%5E2%28A%29+-+cos%5E2%28A%29 = -cos%282A%29 = -sqrt%281+-+sin%5E2%282A%29%29.


Substitute here sin%5E2%282A%29  from (1)  and continue


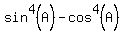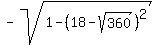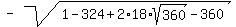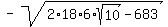sin%5E4%28A%29+-+cos%5E4%28A%29 = -sqrt%281+-+sin%5E2%282A%29%29 = -sqrt%281+-+%2818+-+sqrt%28360%29%29%5E2%29 = -sqrt%281+-+324+%2B2%2A18%2Asqrt%28360%29+-+360%29 = -sqrt%282%2A18%2A6%2Asqrt%2810%29+-+683%29 = 


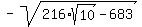= -sqrt%28216%2Asqrt%2810%29-683%29 = -0.228 (approximately, with 3 correct decimal places).


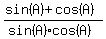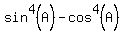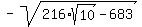ANSWER.  If  %28sin%28A%29+%2B+cos%28A%29%29%2F%28sin%28A%29%2Acos%28A%29%29 = 1%2F3,  then  sin%5E4%28A%29+-+cos%5E4%28A%29 = -sqrt%28216%2Asqrt%2810%29-683%29 = -0.228 (approximately, with 3 correct decimal places).

Solved.