.
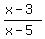 >= 0.
In this problem, there are two values of x, where the binomials in the numerator and denominator change their signs.
These values are x= 3 and x= 5.
Notice that the domain of this inequality is the entire number line except of the value x= 5, where the denominator is zero.
The values (the points) 3 and 5 divide the number line (or, better to say, the domain) in three intervals:
-infinity < x <=3; 3 <= x < 5 and 5 < x < infinity.
At the interval -infinity < x <=3, the numerator (x-3) is negative; the denominator (x-5) is negative, too;
hence, the fraction is positive. Thus the entire interval (
>= 0.
In this problem, there are two values of x, where the binomials in the numerator and denominator change their signs.
These values are x= 3 and x= 5.
Notice that the domain of this inequality is the entire number line except of the value x= 5, where the denominator is zero.
The values (the points) 3 and 5 divide the number line (or, better to say, the domain) in three intervals:
-infinity < x <=3; 3 <= x < 5 and 5 < x < infinity.
At the interval -infinity < x <=3, the numerator (x-3) is negative; the denominator (x-5) is negative, too;
hence, the fraction is positive. Thus the entire interval ( ,
, ] is the part of the solution.
At the interval 3 <= x < 5, the numerator (x-3) is positive; the denominator (x-5) is negative;
hence, the fraction is negative. Thus the entire interval [
] is the part of the solution.
At the interval 3 <= x < 5, the numerator (x-3) is positive; the denominator (x-5) is negative;
hence, the fraction is negative. Thus the entire interval [ ,
, ) is NOT the part of the solution.
At the interval 5 < x < infinity, the numerator (x-3) is positive; the denominator (x-5) is positive;
hence, the fraction is positive. Thus the entire interval (
) is NOT the part of the solution.
At the interval 5 < x < infinity, the numerator (x-3) is positive; the denominator (x-5) is positive;
hence, the fraction is positive. Thus the entire interval ( ,
, ) is the part of the solution.
ANSWER. The solution to the given inequality is the union of two intervals (
) is the part of the solution.
ANSWER. The solution to the given inequality is the union of two intervals ( ,
, ] U (
] U ( ,
, ).
).