Question 1133220: x/x+1 > 5
Solve for x.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As you show the inequality (x/x+1 > 5), x/x is equal to 1, so the inequality says 1+1 > 5. Obviously that is not true; the solution set it the empty set.
So I will assume that the inequality is in fact x/(x+1) > 5.
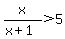
To solve the inequality, we need to have 0 on one side:

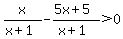
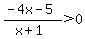
The numerator is 0 when x = -5/4; the function value is 0 there.
The denominator is 0 when x = -1; the function value is undefined there.
Between, negative infinity and -5/4, the numerator is positive and the denominator is negative; the function value is negative.
between -5/4 and -1, the numerator and denominator are both negative; the function value is positive.
Between -1 and infinity, the numerator is negative and the denominator is positive; the function value is negative.
Then, since the inequality is for positive, and since the function is 0 at -5/4 and undefined at -1, the solution set is (-5/4,-1).
|
|
|