Question 1133185: A large piece of paper is 1/64 cm thick. The paper is torn in half and the two pieces placed one on top of the other in a pile.
These are torn in half again and the pieces placed in a pile.
This procedure is continued.
1. How many tears would be necessary to obtain a pile 1 cm high?
A 64
B 16
C 8
D 6
Found 3 solutions by MathLover1, Alan3354, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A large piece of paper is 1/64 cm thick. The paper is torn in half and the two pieces placed one on top of the other in a pile.
These are torn in half again and the pieces placed in a pile.
This procedure is continued.
1. How many tears would be necessary to obtain a pile 1 cm high?
=======================
Each tear doubles the height of the pile.
---> 1/32, 1/16, 1/8, 1/4, 1/2, 1 cm
--> 6 tears.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A large piece of paper is 1/64 cm thick. The paper is torn in half and the two pieces placed one on top of the other in a pile.
These are torn in half again and the pieces placed in a pile.
This procedure is continued.
1. How many tears would be necessary to obtain a pile 1 cm high?
A 64
B 16
C 8
D 6
64 TEARS from one person who responded is wrong!! 64 is the NUMBER of pieces in the pile after 6 tears/cuts (CHOICE D) are made!
And, since each piece is 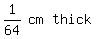 , it follows that a height this is ( , it follows that a height this is (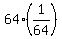 ), or 1 cm will be reached. ), or 1 cm will be reached.
|
|
|