Question 1133134: Draw the following angle in standard position.
225°
a) Name a point on the terminal side of the angle.
(0, −1)
(1, −1)
(1, 1)
(−1, −1)
(−1, 1)
(b) Find the distance d from the origin to that point.
d =
(c) Name another angle that is coterminal with the angle you have drawn.
Answer by Theo(13342)   (Show Source): (Show Source):
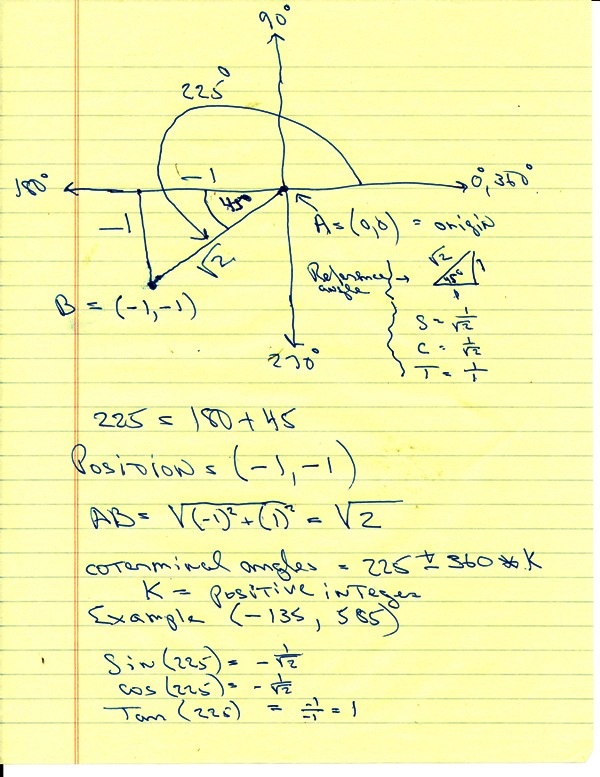
You can put this solution on YOUR website! the position on the graph of 225 degrees is a line from the origin to the point (-1,-1).
that would be equal to 180 + 45 degrees.
the reference angle is 45 degrees.
every time you add 360 degrees to 225, the angle will be in the same position on the graph.
every time you subtract 360 degrees from 225, the angle will be in the same position on the graph.
angles greater than 225 can be any angle that is k * 360 degrees more than 225.
angles less than 225 can be any angle that is k * 360 degrees less than 225.
k can be any positive integer.
all those angles will have the same value for their trigonometric functions as the angle at 225 degrees.
one other angle that is co-terminal with 225 would be 225 + 360 = 585.
another angle that is co-terminal with 225 would be 225 - 360 = -135.
all of the value of the trig functions for these angles will be identical to the value of the trig functions for 225.
example:
sine of (225) = sine of (-135) = sine of (585) = -.7071067812
cosine of (225) = sine of (-135) = cosine of (585) = -.7071067812.
tangent of (225) = sine of (-135) = cosine of (585) = 1.
since 45 degrees is the reference angle, it will have the same value for its trigonometric functions, only they will be all positive.
sine and cosine of (45) = .7071067812.
tangent of (45) = 1.
this is what the angle of 225 degrees looks like on the graph.
|
|
|