SOLUTION: Terry mother figures that she will need to have $200 000 at the end of 10 years. The retirement fund that she has chosen earns interest at 6% compounded semi-annually. A) How mu

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: Terry mother figures that she will need to have $200 000 at the end of 10 years. The retirement fund that she has chosen earns interest at 6% compounded semi-annually. A) How mu      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1133083: Terry mother figures that she will need to have $200 000 at the end of 10 years. The retirement fund that she has chosen earns interest at 6% compounded semi-annually.
A) How much does she need to invest in the fund every six months?
B) how much interest will Terrys mother have earned over the course of her investment?
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
Terry's mother figures that she will need to have $200 000 at the end of 10 years.
The retirement fund that she has chosen earns highlight%28annual%29 interest at 6% compounded semi-annually.
A) How much does she need to invest in the fund every six months?
B) how much interest will Terry's mother have earned over the course of her investment?
~~~~~~~~~~~~~~~~~~~~~~~


            Pay attention on how I edited your post to make it precisely correct. 


It is a classic Ordinary Annuity saving plan. The general formula is 


    FV = P%2A%28%28%281%2Br%29%5En-1%29%2Fr%29,    


where  FV is the future value of the account;  P is the semi-annual payment (deposit); r is the semi-annual percentage yield presented as a decimal; 
n is the number of deposits (= the number of years multiplied by 2, in this case).


From this formula, you get for the semi-annual payment 


    P = FV%2A%28r%2F%28%281%2Br%29%5En-1%29%29.     (1)


Under the given conditions, FV = $200,000;  r = 0.06/2;  n = 10*2 = 20.  So, according to the formula (1), you get for the semi-annual payment 


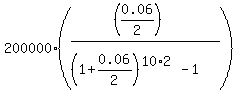    P = 200000%2A%28%28%280.06%2F2%29%29%2F%28%281%2B0.06%2F2%29%5E%2810%2A2%29-1%29%29%29 = $7443.14.


Answer to question (A) :    The necessary semi-annual deposit value is $7443.14.



Note that of projected $200,000 the total of mother's deposits will be only  10*2 times $7443.14, i.e. 10*2*7443.14 = 148862.80 dollars.


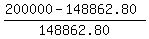Answer to question (B) :  The interest mother will have earned over the course of her investment is  %28200000+-+148862.80%29%2F148862.80 = 34.35%.

---------

On Ordinary Annuity saving plans,  see the lessons
    - Ordinary Annuity saving plans and geometric progressions
    - Solved problems on Ordinary Annuity saving plans
in this site.

The lessons contain  EVERYTHING  you need to know about this subject,  in clear and compact form.

When you learn from these lessons,  you will be able to do similar calculations in semi-automatic mode.