Question 1133048: Use inverse trigonometric functions to find the solutions of the equation that are in the given interval, and approximate the solutions to four decimal places. (Enter your answers as a comma-separated list.)
5 sin 2x = −7.5 cos x; [0, 2π)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is:
5 * sin(2x) = -7.5 * cos(x) and you are looking for a solution in the interval os [0,2 * pi].
sin(2x) is equivalent to 2 * sin(x) * cos(x), therefore you can replace it with that to get:
5 * 2 * sin(x) * cos(x) = -7.5 * cos(x)
divide both sides of that equation by cos(x) and it becomes:
5 * 2 * sin(x) = -7.5
divide both sides of that equation by (5 * 2 = 10) and it becomes:
sin(x) = -7.5 / 10
simplify to get:
sin(x) = -.75
solve for x to get:
arcsin(-.75) = x
use your calculator to get:
x = -48.59037789.
you want the angle to be positive, so add 360 to it until it becomes positive and is between 0 and 360 degrees.
adding 360 to it, you get x = 311.4096221 degrees.
the equivalent angle in the first quadrant would be 360 minus 311.4096221 degrees = 48.59037789.
that's your reference angle.
the sine will be positive when the angle is in the first quadrant.
sin(48.59037789) = .75
you want the sine to be negative.
the sine is negative in the third and fourth quadrant.
the equivalent angle in the third quadrant is the angle in the first quadrant plus 180 degrees.
that makes the equivalent angle in the third quadrant equal to 228.5903779 degrees.
the equivalent angle in the fourth quadrant is 360 minus the angle in the first quadrant.
that makes theequivalent angle in the fourth quadrant equal to 311.4096221 degrees.
if you use your calculator in degree mode, you will find that:
sin(228.5903779) = -.75 and sin(311.4096221) = -.75
so far we've been working in degrees.
to work in radians, you'll do the same thing, only you need to set your calculator to radian mode.
you started with sin(x) = -.75.
use the arcsine function of your calculator in radian mode and it will tell you that x = -.848062079.
you want your angle to be positive between 0 and 2pi radians.
2pi radians are equal to 6.283185307 radians.
add 2 * pi radians to -.848062079 radians to get:
x = 5.435123228 radians.
that angle is in the fourth quadrant.
the equivalent angle in the first quadrant would be 2 * pi radians minus 5.435123228 radians toget:
x = .848062079 radians.
that's the equivalent angle in the first quadrant which would be called the reference angle.
the sine of that angle will be .75.
it is positive because all trig functions for an angle in the first quadrant are positive.
sine is negative in the third quadrant and the fourth quadrant.
the equivalent angle in the third quadrant would be pi + the angle in the first quadrant.
the equivalent angle in the third quadrant is therefore equal to 3.989654733 radians.
the equivalent angle in the fourth quadrant wouldbe 2 * pi - the angle in the first quadrant.
the equivalent angle in the fourth quadrant is therefore equal to 5.435123228 radians.
sin(3.989654733) = -.75
sin(5.435123228) = -.75
the angle in radians is equal to the angle in degrees * pi / 180.
the angle in degrees is equal to the angle in radians * 180 / pi.
your solution in degrees is:
sin(228.5903779) = -.75 and sin(311.4096221) = -.75
your solution in radians is:
sin(3.989654733) = -.75 and sin(5.435123228) = -.75
multiply the degrees shown by pi / 180 and you will get the radians.
multiply the radians shown by 180 / pi and you will get the degrees.
for example:
228.5903779 * pi / 180 = 3.989654733 radians.
3.989654733 radians * 180 / pi = 228.5903779 degrees.
graphically, your solutions will look like this.
the first graph is in degrees.
the second graph is in radians.
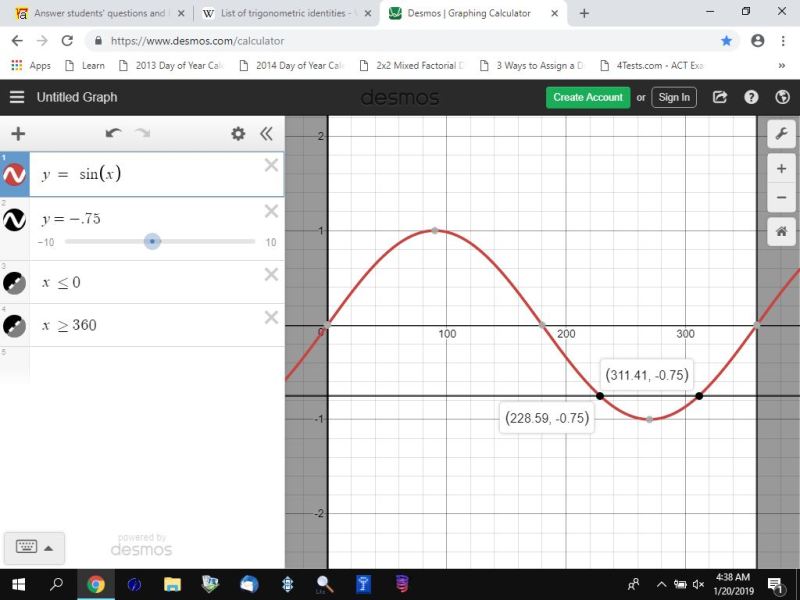

the basic procedue is to graph y = sin(x) and y = -.75.
the intersection of the graph of those two equations is the solution.
working in radians is not as intuitive as working in degrees, but you should get used to it because most higher math courses will work in radians.
if you get confused, then work it in degrees and then convert to radians after.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by tutor @Theo is incomplete (and, therefore, is incorrect).
The method which he uses has a hole, which makes it dangerous.
Therefore, I came to provide a correct solution.
Solution
5*sin(2x) = -7.5*cos(x). (1)
Use a general trigonometry identity for sine of the double angle
sin(2x) = 2*sin(x)*cos(x).
Substitute it into the original equation (1) to get
5*2*sin(x)*cos(x) = -7.5*cos(x)
10*sin(x)*cos(x) + 7.5*cos(x) = 0 (2)
Factor left side
10*cos(x)*(sin(x) + 0.75) = 0. (3)
Divide both sides by 10
cos(x)*(sin(x) + 0.75) = 0. (4)
Notice that at every step my transformations were equivalent, so equation (1) is EQUIVALENT to equation (4).
In other words, equations (1) and (4) have the same set of solutions.
Now, equation (4) deploys in two independent equations:
(a) cos(x) = 0, and
(b) sin(x) + 0.75 = 0, or, equivalently, sin(x) = -0.75.
It means that the solution set to equation (4) is the union of solutions to equations (a) and (b).
For equation (a) the solutions in the given interval are x= arccos(0) =  = 1.5708 and x= arccos(0) + = 1.5708 and x= arccos(0) +  = = 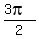 = 4.7124.
For equation (b) the solutions in the given interval are x= arcsin(-0.75) + = 4.7124.
For equation (b) the solutions in the given interval are x= arcsin(-0.75) +  = 5.4351 and x = arcsin(0.75) + pi = 3.9897.
ANSWER. The given equation has 4 solutions in the interval [ = 5.4351 and x = arcsin(0.75) + pi = 3.9897.
ANSWER. The given equation has 4 solutions in the interval [ , , ). They are
x= ). They are
x=  = 1.5708, x= = 1.5708, x= 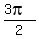 = 4.7124, x= arcsin(-0.75) + = 4.7124, x= arcsin(-0.75) +  = 5.4351 and x= arcsin(0.75) + = 5.4351 and x= arcsin(0.75) +  = 3.9897.
Numerical values are in radians and are correct with 4 decimal places, as the problem does request. = 3.9897.
Numerical values are in radians and are correct with 4 decimal places, as the problem does request.
The solution is completed.
-----------------------
The lessons to learn from my solution are THESE :
(a) You can not divide equations (2) and (3) by cos(x) without analyzing the case cos(x) = 0.
Otherwise, you loose the solutions of the equation cos(x) = 0.
(b) If you do it (if you divide equations (2) and (3) by cos(x) without analyzing the case cos(x) = 0),
it is traditionally considered as a RUDE MISTAKE, showing that you don't know the rules of solution of such equations.
So, doing in this way and making this error, you INEVITABLY loose your scores at an exam.
|
|
|