Question 1133039: hallar la ecuacion de las hiperbolas determinadas por:
1) vertices (+-1,0) asíntotas y=+-5x
2) focos (0,+-6) pasa por P=(-5,9)
3) focos (0,+-1) longitud eje real:1
4) asíntotas y= +- x/2 pasa por el punto de coordenadas (5,2)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Standard form:
 ->Transverse axis is horizontal ->Transverse axis is horizontal
 -.>Transverse axis is vertical -.>Transverse axis is vertical
1)
given:
Vertices: ( , ,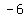 ), ( ), ( , , ) =>Semi-major axis length: ) =>Semi-major axis length: 


First asymptote: 
Second asymptote: 
=> Transverse axis is vertical
Standard form: 
intersection of the asymptotes is at origin:
so, center is at: ( , , ) => ) =>  and and 
=>
From the original equations of asymptotes, you can determine the slopes of the asymptotes to be  and and 
since  and and  , we have , we have

=>



2.
2) focos (0,+-6) pasa por P=(-5,9)
the coordinates of the foci are ( ,± ,± ) )
foci lie on y axis, so your formula is:

=>  or or 



P=( , , ) )
 => round it to => round it to 
 => round it to => round it to 







3) focos (0,+-1) longitud eje real:1
longitud eje real:1=> the length transverse axis is 
=>
=>
the coordinates of the foci are ( ,± ,± ) => ) =>  =± =± and and
foci lie on  axis, so your formula is axis, so your formula is

=>  or or 






4) asíntotas  = ± = ±  pasa por el punto de coordenadas (5,2) pasa por el punto de coordenadas (5,2)
 = ± = ± 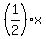
intersection of the asymptotes is at origin:
so, center is at: ( , , ) => ) =>  and and 
asymptotesup-down  = ± = ± 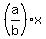


since passes through ( , , ) )










|
|
|