SOLUTION: Use the formula for the probability of the complement of an event. Two dice are tossed. What is the probability of getting a sum of at least 3? (Enter your probability as a frac

The full space of events is the set of all pairs (m,n), where m and n are integers between 1 and 6 inclusively 
- possible outcomes from each dice.


Thus the full space of events has 6*6 = 36 elements, each with the probability of .


The probability of getting the sum at least of 3 is the sum of probabilities of getting 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 (maximum).


The complement event is to get the sum of 2, which is possible for only one configuration (m,n) = (1,1) of the base space of events.


So, the probability of getting this complement event is  .


Hence, the probability that the problem asking for is 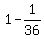  = 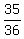.     ANSWER