Question 1132863: In a class, half of the students took Geography while three-fifths took Statistics. If 8 students took both and four students did not choose any of the two subjects, how many students are there in class?
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
Let x be the number of students in the class.
There are two ways to calculate the number of those who study at least one subject, Geography OR Statistics.
From one side, this number is N = (x-4).
From the other side, this number is
N = 0.5x + 0.6x - 8.
Indeed, 0.5x represents the half of student in the class, who take Geography.
0.6x represents three-fifth of the students in the class, who take Statistics.
And I subtracted 8 from the sum, who take both classes and whom I calculated twice, when added 0.5x and 0.6x.
It gives me an equation
x - 4 = 0.5x + 0.5x - 8
to find x.
So, I simplify the equation
8 - 4 = 0.5x + 0.6x - x
4 = 0.1x
and obtain the
ANSWER. There are x= 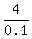 = 40 students in the class.
Solved, explained, answered and completed.
|
|
|
