SOLUTION: The length of one of the equal legs of an isosceles triangle is 8cm less than the length of the base. If the perimeter is 29cm, find the length of one of the equal legs. What I hav

Algebra ->  Linear-equations -> SOLUTION: The length of one of the equal legs of an isosceles triangle is 8cm less than the length of the base. If the perimeter is 29cm, find the length of one of the equal legs. What I hav      Log On


   

Question 113273: The length of one of the equal legs of an isosceles triangle is 8cm less than the length of the base. If the perimeter is 29cm, find the length of one of the equal legs. What I have so far is this, 4x+(2x-8)=29cm.
Thank you for you help,
Barb Neely
Found 3 solutions by jim_thompson5910, Earlsdon, solver91311:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Let x=length of base, y=length of equal legs

Since one of the equal legs is 8 cm less than four times the base the base, we get

Equal Leg: y=4x-8


Now simply add the base to two equal legs like this:

x%2By%2By=29

x%2B2y=29 Combine like terms


x%2B2%284x-8%29=29 Plug in y=x-8




x%2B8x-16=29 Distribute


9x-16=29 Combine like terms on the left side


9x=29%2B16Add 16 to both sides


9x=45 Combine like terms on the right side


x=%2845%29%2F%289%29 Divide both sides by 9 to isolate x



x=5 Divide

--------------------------------------------------------------
Answer:
So our answer is x=5


So this means the base is 5 cm

4%2A5-8=20-8=12 Now plug in x=5 into y=4x-8 to find the equal leg's length.


So the equal legs are 12 cm each


Check:

The sum of the sides should be 29, so let's verify:

5%2B12%2B12=29 Plug in the solved values into the perimeter formula


29=29 Add. Since both sides are equal, our answer is verified.


Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
I don't quite understand how you arrived at: 4x+(2x-8) = 29 cm?
Let the length of the base be x, then the length of one of the equal sides is x-8.
So you can express the perimeter of this triangle by: P+=+S%5B1%5D%2BS%5B2%5D%2BS%5B3%5D
P = (x-8) + (x-8) + x Simplifying this we get:
P = 3x-16 but the problem says that this is equal to 29 cm, so...
29 = 3x-16 Add 16 to both sides.
45 = 3x Divide both sides by 3.
15 = x
So the base is 15 cm in length.
The sides are x-8 or 15 - 8 = 7 cm.
So the answer is 7 cm.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
I've pushed and shoved this one several ways and I can't seem to get to the expression 4x%2B%282x-8%29=29. So the only thing I know to do at this point is start from the beginning.

We want to find the length of one of the equal legs, so let's call that x. We also know that the other equal leg has to be x as well, and we are told that x is 8 cm less than the base. That means we can express the length of the base as x + 8.

The perimeter of any geometric figure is simply the sum of the lengths of all its sides, so we can express that in this case by saying:

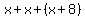x%2Bx%2B%28x%2B8%29, which we know to be equal to 29 cm. Therefore,

x%2Bx%2B%28x%2B8%29=29
3x%2B8=29
3x=21
x=7, which is the length of one of the equal legs.

Check:

The base must be 7 + 8 = 15 cm, so the perimeter must be 7 + 7 + 15 which does, in fact, equal 29. The answer checks.

Hope this helps,
John