Question 1132726: how do you solve the system of equations using substitution?
3y=-7x+10
3y=4x+38
Found 3 solutions by MathLover1, Alan3354, ikleyn:
Answer by MathLover1(20850)   (Show Source):
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! how do you solve the system of equations using substitution?
3y=-7x+10
3y=4x+38
------------
Sub for 3y in the 2nd eqn.
---
3y=4x+38
-7x+10 = 4x+38
11x = -28
x = -28/11
=============
3y=4x+38
3y = -112/11+38 = -112/11 + 418/11
3y = 306/11
y = 102/11
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
It can be done in much simpler way, and you deserve to know it . . .
From the first equation, you just have the expression for 3y: it is -7x + 10.
Substitute it into the second equation in whole, as is, replacing 3y in its left side by -7x + 10.
You will get
-7x + 10 = 4x + 38. (*)
It is how the substitution method works in this case (or, it is the way on how YOU CAN USE the substitution method in this case).
So, you MOMENTARILY obtain a single equation for one unknown x, which you easily can solve. From (*), you have
10 - 38 = 4x + 7x
-28 = 11x ====> x =  .
As the next and last step, you substitute the found value of x into either of the two given equations to determine y.
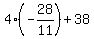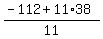3y =  =  =  ====> y =  =  .
ANSWER. x = , y = .
Solved // by using the substitution method // in its economic mode.
--------------
For other similar solved problems, see the lesson
- Useful tricks when solving systems of 2 equations in 2 unknowns by the Substitution method
in this site.
|
|
|
