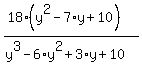 First we factor the numerator as 18(y-2)(y-5)
Factor the denominator by the ±p/q method
Try 2 as as a zero of the denominator, using
synthetic division:
2 | 1 -6 3 10
| 2 -8 -10
1 -4 -5 0
So the denominator factors as (y-2)(y²-4y-5) which
factors completely as (y-2)(y-5)(y+1)
So the expression becomes:
First we factor the numerator as 18(y-2)(y-5)
Factor the denominator by the ±p/q method
Try 2 as as a zero of the denominator, using
synthetic division:
2 | 1 -6 3 10
| 2 -8 -10
1 -4 -5 0
So the denominator factors as (y-2)(y²-4y-5) which
factors completely as (y-2)(y-5)(y+1)
So the expression becomes:
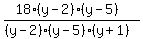 We cancel, but observe that y cannot be 2,5,-1,
for they would make the denominator 0.
We cancel, but observe that y cannot be 2,5,-1,
for they would make the denominator 0.
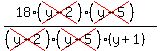
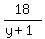 For that to be an integer, the denominator must be a factor
of the numerator 18.
The integer factors of 18 are ±1,±2,±3,±6,±9,±18
So the denominator y+1 must be one of those in order
for the expression to be an integer:
We take positive and negative values separately:
The positive values:
y+1 = 1, 2, 3, 6, 9, 18
y = 0, 1, 2, 5, 8, 17
But as we said above, we must eliminate 2 and 5 from the
list of permissible values of y, so when y is positive,
it must be one of these values:
y = 0, 1, 8, 17
The negative values:
y+1 = -1,-2,-3,-6, -9,-18
y = -2,-3,-4,-7,-10,-19
All those are permissible values of y.
So all values of y which cause the original
expression to be an integer are
0, 1, 8, 17,-2,-3,-4,-7,-10,-19
Sum = 0+1+8+17-2-3-4-7-10-19 = -19
Edwin
For that to be an integer, the denominator must be a factor
of the numerator 18.
The integer factors of 18 are ±1,±2,±3,±6,±9,±18
So the denominator y+1 must be one of those in order
for the expression to be an integer:
We take positive and negative values separately:
The positive values:
y+1 = 1, 2, 3, 6, 9, 18
y = 0, 1, 2, 5, 8, 17
But as we said above, we must eliminate 2 and 5 from the
list of permissible values of y, so when y is positive,
it must be one of these values:
y = 0, 1, 8, 17
The negative values:
y+1 = -1,-2,-3,-6, -9,-18
y = -2,-3,-4,-7,-10,-19
All those are permissible values of y.
So all values of y which cause the original
expression to be an integer are
0, 1, 8, 17,-2,-3,-4,-7,-10,-19
Sum = 0+1+8+17-2-3-4-7-10-19 = -19
Edwin