SOLUTION: A tank holds 80 liters of a chemical solution. Currently, the solution has a strength of 30%. How much of this solution must be DRAINED and REPLACED with a 70% solution to get a st

Let W be the volume to drain off from 80 liters of solution.


Step 1:  Draining.  After draining,  you have (80-W) liters of the 30% acid solution.



Step 2:  Replacing.  Then you add W liters of the 70% solution (the replacing step).

                     After the replacing,  you have the same total liquid volume of 80 liters.


It contains  0.3*(80-W) + 0.7*W   of pure solvent.



So, your "concentration equation" is


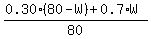     = 0.4.    (1)



At this point, the setup is done and completed.



Now you need to solve your basic equation  (1).

As the first step, multiply both sides by 80, and then simplify


    0.30*(80-W) + 0.7*W = 0.4*80

    24 - 0.3W + 0.7W = 32

    0.4W = 32 - 24 = 8

    W =  = 20.


ANSWER.  20 liters of the original 30% solution should be drained and replaced by 20 liters of the 70% solutions.


CHECK. 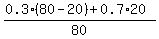   = 0.4.    ! Precisely correct !