SOLUTION: If a^2+b^2=7ab,prove that log{1/3(a+b)}=1/2(log a + log b)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: If a^2+b^2=7ab,prove that log{1/3(a+b)}=1/2(log a + log b)       Log On


   

Question 1132319: If a^2+b^2=7ab,prove that log{1/3(a+b)}=1/2(log a + log b)
Answer by ikleyn(52899) About Me  (Show Source):
You can put this solution on YOUR website!
.

            The given condition is not completed.  To be complete,  it must be re-edited in this way: 

            If a^2+b^2 = 7ab,  where "a" and "b" are positive real numbers,  prove that log{1/3(a+b)}=1/2(log a + log b).

            With this re-editing,  the solution/(the proof) is as follows. 


If   a^2 + b^2 = 7ab   then


a^2 + 2ab + b^2 = 9ab


(a + b)^2 = 9ab


log((a+b)^2) = log(9ab)


2*log(a+b) = log(9) + log(a) + log(b)


2*log(a+b) = 2*log(3) + log(a) + log(b)


2*(log(a+b) - log(3)) = log(a) + log(b)


log(a+b) - log(3) = %281%2F2%29%2A%28log%28%28a%29%29+%2B+log%28%28b%29%29%29
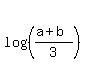log%28%28%28a%2Bb%29%2F3%29%29 = %281%2F2%29%2A%28log%28%28a%29%29+%2B+log%28%28b%29%29%29.

QED.   The proof is completed.