Question 1132292: Find the area of an equilateral triangle inscribed in a circle circumscribed by a square made by joining the mid points of the adjacent sides of a square of side "a" ?
Found 2 solutions by addingup, greenestamps:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! square made by joining the mid points of the adjacent sides of a square of side "a":
a/2 = side of circumscribing square
sqrt[(a/2)^2 + (a/2)^2] = any one of the sides of the circumscribing square: E F, F G, G M, H E.
Any one of these, let's take F G, is the diameter of the circle circumscribed by the square
.
Side of circumscribing square = diameter circle
To solve from here, apply Heron's formula, then a little trigonometry, and you're done. Here is a picture I made you to help you:
.

Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) The area of the small square is half the area of the large square. (You can see this by drawing just the two squares and then drawing the diagonals of the small square.) So the side length of the small square is 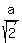 . .
(2) The side length of the small square is the diameter of the circle.
(3) Obviously the radius of the circle is half its diameter.
(4) By drawing the three altitudes of the equilateral triangle (dividing the triangle into 6 congruent 30-60-90 right triangles), you can determine that the side length of the triangle is (sqrt(3)/2) times the radius of the circle.
Put all those part together to find the side length of the triangle; then the area of an equilateral triangle with side length s is 
|
|
|