SOLUTION: The number of all pairs (m,n) are positive integers such that 1/m + 1/n + 1/mn = 2/5 ?

Algebra ->  Number-Line -> SOLUTION: The number of all pairs (m,n) are positive integers such that 1/m + 1/n + 1/mn = 2/5 ?      Log On


   

Question 1132290: The number of all pairs (m,n) are positive integers such that 1/m + 1/n + 1/mn = 2/5 ?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

The number of all pairs (m,n) are positive integers such that
1%2Fm+%2B+1%2Fn+%2B+1%2Fmn+=+2%2F5+
n%2Fmn+%2B+m%2Fnn+%2B+1%2Fmn+=+2%2F5+
%28n%2B+m%2B+1%29%2Fmn+=+2%2F5+
5%28n%2B+m%2B+1%29+=+2mn+
5n%2B+5m%2B+5=+2mn+
5n-2mn=-%285m%2B+5%29+
%285-2m%29n=-5%28m%2B+1%29+
-%282m-5%29n=-5%28m%2B+1%29+
n+=+%285+%28m+%2B+1%29%29%2F%282+m+-+5%29
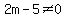
=>2+m+-+5%3C%3E0
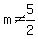
=>m+%3C%3E5%2F2
(5%2F2, infinity) => since we need positive integers, they are:1,2,34,....infinity
n+=+%285+%280+%2B+1%29%29%2F%282+%2A0+-+5%29
n+=+-1
(-1, infinity)=> since we need positive integers, they are:1,2,34,....infinity
positive integers will be:
try them out and you will find these pairs:
m+=+3, n+=+20
m+=+5, n+=+6
m+=+6, n+=+5
pairs (m,n) are
(3,20), (5,6), (6,5)

Answer by ikleyn(52903) About Me  (Show Source):
You can put this solution on YOUR website!
.
I agree with the analysis by the tutor @MathLover1.


I only want to add that together with the pair (m,n) = (3,20), the pair (m,n) = (20,3) is also the solution.


It is clear from the fact that the original equation is symmetric relative "m" and "n".


So, the solutions are these 4 pairs  (m,n) = (5,6), (6,5), (3,20) and (20,3).