|
Question 1132266: a university alumni association invested part of 200,000 in preferred stock that earns 8% annual simple interest, and the remainder in a municipal bond that earns 7% annual simple interest. The amount of interest earned each year is 15200. How much was invested in each account?a university alumni association invested part of 200,000 in preferred stock that earns 8% annual simple interest, and the remainder in a municipal bond that earns 7% annual simple interest. The amount of interest earned each year is 15200. How much was invested in each account?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Notice that the problem formulation and the question were doubled in the post.
Also be advised that posting the correct input ONE TIME is enough: there is no any need to post it twice . . .
Solution
Let x = the amount invested at 8%;
then the amount invested at 7% is the rest (200000-x).
Your equation is
interest + interest = total interest, or
0.08x + 0.07*(200000-x) = 15200.
Simplify and solve for x.
ANSWER. x = 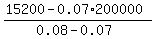 = 120000. = 120000.
Solved.
-------------------
It is a standard and typical problem on investments.
If you need more details, or if you want to see other similar problems solved by different methods, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is an alternative to the standard algebraic method for solving "mixture" problems like this. It involves only a few simple calculations, so you can get to the answer much faster than by setting up and solving an algebraic equation.
(1) If all the money were invested at 7%, the interest would be 14000; if all were invested at 8%, the interest would be 16000.
(2) The actual amount of interest, 15200, is three-fifths of the way from 14000 to 16000. (15200-14000 = 1200; 16000-14000 = 2000; 1200/2000 = 3/5)
(3) That means 3/5 of the money (120000) was invested at the higher rate.
ANSWER: 120000 at 8%; 80000 at 7%.
|
|
|
| |