SOLUTION: O, is the centre of circle HKL. Side HK= 16cm, side HL = 10cm and the perpendicular from O to HK is 4cm. With the aid of a diagram what is the lenght of the perpendicular from O t

Draw in radii OK, OH and OL and let their lengths be r.
Let OA = 4, the perpendicular from O to HK.
Let the red line OB = x, the perpendicular from O to HL, the length
of which is what we are to find.

Triangle OHK is isosceles, so the perpendicular from O to HK, which 
is 4, bisects the base HK.  HK is given as 16, so AH = AK = 8.

Similarly, triangle OHL is isosceles, so the perpendicular from O to HL,
which is our unknown x, bisects the base HL.  HL is given as 10, so 
BH = BL = 5.

 

We use the Pythagorean theorem on either right triangle OAH or OAK:

r² = 8²+4² = 64+16 = 80
 
We use the Pythagorean theorem on either right triangle OBH or OBL:

r² = x²+5², and we have already found r² = 80, so

80 = x²+25

55 = x²



So the solution is 

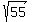Edwin