SOLUTION: The sum of the first n terms of a G.P. is 255 and the sum of their reciprocal is 255/128. If the first term is 1. Find n and the common ratio.

Let r be the common ratio and n be the number of terms.

Then the sum of the first n terms of the first GP is  A = 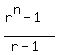,  which gives first equation

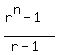     = 255.           (1)


The second sequence is a geometric progression, too. Its common ratio is  , which is OBVIOUS.

The sum of the first n terms of the second GP is  A =  = ,  which gives the second  equation

     = .       (2)


Now divide eq(1) by eq(2)  (both sides).  You will get


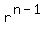     = 128.           (3)


At this point, there is a big desire to conclude that r= 2 and n= 8.
But do not hurry:  we still have no solid base for making such conclusion.

We need to make one more, last step in the solution.


From eq(3), substitute the value 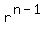   = 128  into equation (1). You will get then


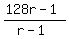     = 255,

    128r - 1 = 255*(r-1)

    128r - 1 = 255r - 255

    255 - 1 = 255r - 128r

    254     = 127r  =================>  r =  = 2.


Now we may easily conclude from (3)  that  n-1 = 7;  hence,  n= 8.