Question 1131994: write out the expansion of (r-s)^5. watch out for that minus sign!
Found 4 solutions by MathLover1, Alan3354, greenestamps, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Expanding this expression algebraically might be a good exercise; but it is very inefficient for this problem.
Expand using the binomial formula. (or Pascal's Triangle, which is essentially the binomial formula)

= 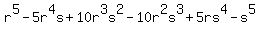
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I want to develop / (to explain) further the idea of using the Pascal triangle.
From the solution by @greenestamps, you see that you need, essentially, only two coefficients 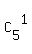 = 5 at x^4 and = 5 at x^4 and 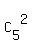 = 10 at x^3.
The other two are the same by the symmetry, and the first and the last coefficients are simply "1".
These two coefficients = 10 at x^3.
The other two are the same by the symmetry, and the first and the last coefficients are simply "1".
These two coefficients 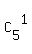 = 5 at x^4 and = 5 at x^4 and 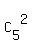 = 10 at x^3 are easy to calculate.
And you do need nothing more.
The Pascal triangle carries the coded arrays of binomial coefficients.
You can see the Pascal triangle, read about its properties and learn about its connections to Binomial expansion from the lesson
- The Pascal's triangle
in this site.
Usually, the students familiar with this subject, know and remember first 5 - 6 lines of the Pascal triangle,
so they can easily write this binomial expansion from their memory till the five degrees binomial expansion.
Besides of this, the Pascal triangle has simple rules and properties allowing to expand it infinitely far quickly and easily,
so it is really useful object and subject to learn and to apply.
Regarding the signs of the binomial coefficients, they simply alternate (+ - + - + -) in this case. = 10 at x^3 are easy to calculate.
And you do need nothing more.
The Pascal triangle carries the coded arrays of binomial coefficients.
You can see the Pascal triangle, read about its properties and learn about its connections to Binomial expansion from the lesson
- The Pascal's triangle
in this site.
Usually, the students familiar with this subject, know and remember first 5 - 6 lines of the Pascal triangle,
so they can easily write this binomial expansion from their memory till the five degrees binomial expansion.
Besides of this, the Pascal triangle has simple rules and properties allowing to expand it infinitely far quickly and easily,
so it is really useful object and subject to learn and to apply.
Regarding the signs of the binomial coefficients, they simply alternate (+ - + - + -) in this case.
H a p p y l e a r n i n g ! !
|
|
|