Question 1131932: Find the perimeter of ΔTAP with vertices T(1, 4), A(4,4), and P(3,0) to the nearest tenth unit.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
the perimeter of Δ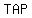 is: is:

find the length which is equal to distance between points
if vertices are at  ( ( , ,  ), ),  ( ( , , ), and ), and  ( ( , , ), we have ), we have
 ...if ...if  ( ( , ,  ), ),  ( ( , , ) )



 ...if ...if  ( ( , ,  ), ), ( ( , , ) )







 .... .... ( ( , , ), ), ( ( , , ) )






 .......to the nearest tenth unit .......to the nearest tenth unit
|
|
|