|
Question 1131751: Points B(b,0) and C(c,10) are to be placed on this graph so that the distance from A to B to C to D is a minimum. Find the value of b.
Note: point A is at (0,4) and point D is at (8,9)
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
---------------------------------------------------------------------
(corrected/revised response 12/15)
Going from A(0,4) to B(b,0) to C(c,10) to D(8,9), the y values go...
down from 4 to 0;
up from 0 to 10; and
down from 10 to 9
Going from A to B to C to D, the x values go from 0 to b to c to 8. The minimum total distance from A to B to C to D will be if we are always moving in the same x direction. Since the starting x value is 0 and the ending x value is 8, we know b and c will be between 0 and 8.
So A to B is a negative slope, B to C is a positive slope, and C to D is a negative slope.
The minimum total length of the path from A to D will be when the three slopes all have the same absolute value.
The slope of AB is 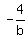 . .
The slope of BC is  . .
The slope of CD is 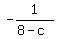 . .
So we need to have equal slopes for AB and CD:


(1) 
And we need to have the slope of BC the opposite of the slope of CD:


(2) 
We can eliminate c between (1) and (2) to find the value of b.
(1) 
(2) 


ANSWER: The minimum distance from A to B to C to D is when b = 32/15.
-----------------------------------------------------------------
(added 12/15)
Perhaps this alternative method of solving the problem makes the solution easier to understand....
We are trying to find the minimum distance from A(0,4) to B(b,0) to C(c,10) to D(8,9). The first leg from A to B has a negative slope; the second from B to C has a positive slope; the third from C to D has a negative slope.
We can make all the slopes positive as follows:
The distance from (0,4) to (b,0) is the same as the distance from (0,-4) to (b,0). So define a new point A'(0,-4).
The distance from (c,10) to (8,9) is the same as the distance from (c,10) to (8,11). So define a new point D'(8,11).
Every leg of the path from A' to B to C to D' now has a positive slope.
The shortest distance from A' to B to C to D' will be the straight line distance from A' to D'.
So to find the value of b, we find the equation of the line A'D' and find the value of b for which (b,0) is on that line.
The slope of line A'D' is (11-(-4))/(8-0) = 15/8; the y-intercept is (0,-4); the equation is

Solving for x when y=0:



|
|
|
| |