SOLUTION: Find the roots of the equation x³ - 9x² + 23x - 15 = 0, if they are in AP.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Find the roots of the equation x³ - 9x² + 23x - 15 = 0, if they are in AP.      Log On


   

Question 1131744: Find the roots of the equation x³ - 9x² + 23x - 15 = 0, if they are in AP.
Found 5 solutions by josgarithmetic, MathLover1, ikleyn, solver91311, greenestamps:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
You can guess, and find them. Rational Roots Theorem will suggest 1, 3, 5, which you can also test using synthetic division...

1, 3, 5.

Answer by MathLover1(20850) About Me  (Show Source):
Answer by ikleyn(52793) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let a, b and c be these roots.

Since they form an AP, we can write them as  m-d, m and m+d, where m is the middle term m=b and d is the common difference,  so

    a = m-d, c = m+d.


Then according to the Vieta's theorem, the sum of the roots is equal to the coefficient at  x%5E2  taken with the opposite sign:

    (m-d) + m + (m+d) = 9,   or   3m = 9,  which implies  m = 9/3 = 3.


The product of the roots, using the Vieta's theorem again, is equal to the constant term taken with the opposite sign:

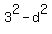    (3-d)*3*(3+d) = 15,   or  3%5E2+-+d%5E2 = 15/3 = 5,  which implies  d%5E2 = 9 - 5 = 4;  hence,  d = +/-sqrt%284%29 = +/-2.


In this way, the AP is  EITHER   3-2 = 1, 3, 3+2 = 5  OR  5, 3, 1,  which makes no difference.


Answer.  The roots are  1, 3 and 5.

Solved.



Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!




3 roots. 3 sign changes for : Maximum 3 positive real roots.



Zero sign changes for : Maximum zero negative real roots.

The lead coefficient is 1, the constant term is -15. Possible rational roots

but the negative values are excluded by the Rule of Signs, so the possible rational roots are

Synthetic Division

5  |  1   -9   23  -15								
           5  -20   15   
   -------------------
      1   -4    3    0






Zeros are 1, 3, and 5

John

My calculator said it, I believe it, that settles it

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The given information that the roots are in AP makes the problem easy.

For the shortest path to the solution, use the rational roots theorem as suggested by tutor @josgarithmetic and Vieta's theorem as suggested by tutor @ikleyn:

(1) The possible rational roots are 1, 3, 5, -1, -3, and -5.
(2) The product of the roots is -(-15/1) = 15; the sum of the roots is -(-9)/1 = 9.

The only possible rational roots that satisfy Vieta's theorem are 1, 3, and 5.

ANSWER: The roots are 1, 3, and 5.