.
First, it is clear that
P =  =
=
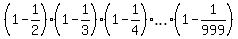 *(
*( Now, consider Q =
Now, consider Q = 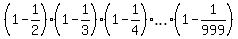 .
Notice that the denominator of the first fraction is the numerator of the second fraction.
Next, the denominator of the second fraction is the numerator of the third fraction.
This pattern continues: the denominator of the third fraction is the numerator of the fourth fraction.
And so on . . .
Cancel all common factors in numerators and denominators to get the value Q =
.
Notice that the denominator of the first fraction is the numerator of the second fraction.
Next, the denominator of the second fraction is the numerator of the third fraction.
This pattern continues: the denominator of the third fraction is the numerator of the fourth fraction.
And so on . . .
Cancel all common factors in numerators and denominators to get the value Q = 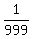 .
Next, consider R =
.
Next, consider R =  .
Notice that the numerator of the first fraction is the denominator of the second fraction.
Next, the numerator of the second fraction is the denominator of the third fraction.
This pattern continues: the numerator of the third fraction is the denominator of the fourth fraction.
And so on . . .
Cancel all common factors in numerators and denominators to get the value R =
.
Notice that the numerator of the first fraction is the denominator of the second fraction.
Next, the numerator of the second fraction is the denominator of the third fraction.
This pattern continues: the numerator of the third fraction is the denominator of the fourth fraction.
And so on . . .
Cancel all common factors in numerators and denominators to get the value R = 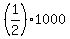 = 500.
So, the final answer is P = Q*R =
= 500.
So, the final answer is P = Q*R =  =
= 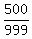 . ANSWER.
. ANSWER.
Solved.