Question 1131290: How many complex, real, and rational roots does the following polynomial have:
2x^5-4x^4-4x^2+5
I think the number of complex roots would be 5, and the number of rational roots would be 4, but am confused about how to find the number of real roots.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given:
 ->It is degree ->It is degree  , so there are , so there are  roots. roots.
we can say how many are 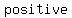 or or  just by counting how many times the sign changes (from plus to minus, or minus to plus) just by counting how many times the sign changes (from plus to minus, or minus to plus)
The number of sign changes is the maximum number of positive roots.
you have:
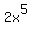 -> sign + -> sign +
 -> sign - which is -> sign - which is 
 -> sign - no change -> sign - no change
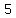 -> sign + which is -> sign + which is 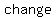
There are  changes in sign, so there are at most changes in sign, so there are at most   roots (maybe less).So there could be roots (maybe less).So there could be  , or , or  , or , or  positive roots. positive roots.
By doing a similar calculation we can find out how many roots are  " in place of " " in place of " ", like this: ", like this:
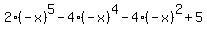
=
Only the odd exponents, like  , , , , , etc will reverse their sign: , etc will reverse their sign:
only 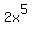 have changed to have changed to 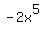
One change only, so there is  negative root. negative root.
So there are at most  positive roots and positive roots and  negative root, there are at most negative root, there are at most 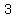 real roots. real roots.
we also know Complex Roots always come in pairs which means we either get:
 complex roots complex roots
 complex roots complex roots
 complex roots, complex roots,
etc
in this case we will have  complex roots because we have at most complex roots because we have at most  real roots real roots

|
|
|