Question 1131289: Prove that no group of order 96 is simple.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

Theorem: Suppose that G is a finite group and p a prime such that np(G)>1, and choose distinct Sylow p-subgroups S and T of G such that the order |S∩T| is as large as possible. Then np(G)≡1(mod|S:S∩T|)
Applying this for |G|=96 and p=2 (assuming n[2](G)=3, otherwise we are done), we see that
|S:S∩T|=2.
Let D=S∩T, so D is normal in S and T.
Hence both S and T lie in the normalizer NG(D).
But S and T are distinct, hence |NG(D)|>|S|=25.
This forces NG(D)=G, i.e. D⊲G. We found a nontrivial proper normal subgroup.
or
There is a following generalization of one of the Sylow's theorems (see for example here), which is equivalent to the theorem in Cihan's answer.
Let  , , ,…, ,…,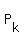 be the Sylow p-subgroups of G. If [ be the Sylow p-subgroups of G. If [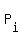 : :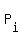 ∩ ∩ ]≥ ]≥ 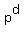 whenever i≠j, then whenever i≠j, then 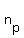 ≡1mod ≡1mod 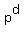
.Taking  gives you one of Sylow's theorems, and the contrapositive of this theorem in the case gives you one of Sylow's theorems, and the contrapositive of this theorem in the case  is useful here. is useful here.
If 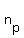 ≢1mod ≢1mod , then there exist different Sylow p-subgroups , then there exist different Sylow p-subgroups  and and with [ with [ : : ∩ ∩ ]< ]< . .
This implies that [ : : ∩ ∩ ]=[ ]=[ : : ∩ ∩ ]= ]= , and thus the intersection , and thus the intersection  ∩ ∩ is normal in both is normal in both  and and  . .
In your problem, we can assume  . Then . Then  ≢1mod ≢1mod , so we find different Sylow 2-subgroups , so we find different Sylow 2-subgroups  and and  with with ∩ ∩ normal in both normal in both  and and  . .
Therefore the intersection  ∩ ∩ is normal in the subgroup ⟨ is normal in the subgroup ⟨ , , ⟩ generated by ⟩ generated by  and and  . The order of ⟨ . The order of ⟨ , , ⟩ is a multiple of ⟩ is a multiple of  and larger than and larger than  , so it has to equal , so it has to equal 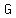 . .
Thus  ∩ ∩ is a nontrivial proper normal subgroup of is a nontrivial proper normal subgroup of . .
|
|
|