SOLUTION: In a triangle ABC with usual notations, show that 2a∙sin²(C/2)+2c∙sin²(A/2) = a-b+c

First we draw a general triangle ABC with the usual notations,
with altitude h to base b, dividing b into two parts x and y, 
such that x+y = b.



[Note that we can always choose the lettering so that the altitude h
is inside the triangle, so that x+y=b.  We can also similarly prove
the proposition when h is outside the triangle. It will only involve
changing some signs.]

We start with the left side:



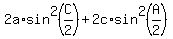Use the half angle formula to substitute for the sines:





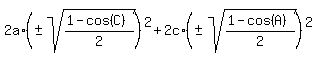Squaring square roots takes them both away:



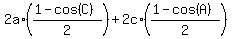Cancel the 2's





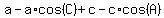Now go back to the triangle up there. From it, we have
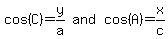 and substitute
the fractions for the cosines:



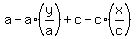Cancel the a's in the second term and the c's in the last term:



Rearrange the terms:



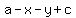Take " - " sign out of the two middle terms:



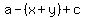And since from the triangle x+y = b, we have
the right side of what was given:



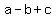Edwin