Question 1130764: Identify the graph that correctly represents the inequality |x + 1| + 2 > 5.
Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The inequality is equivalent to 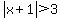
Let's look at two different ways to solve a problem like this.
The standard method, usually taught first, is to break the problem into two cases, depending on whether (x+1) is positive or negative.
(1) If (x+1) is zero or positive, then abs(x+1) is just (x+1). The inequality is then
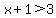

(2) If (x+1) is negative, then abs(x+1) is -(x+1) = (-x-1). The inequality is then
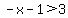
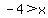 or or 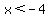
So the solution set for the inequality is  or or 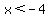 . .
Then here is another way to solve problems involving equations or inequalities with absolute values.
The expression  can be interpreted as meaning that the distance between x and a is equal to b. For many more advanced problems involving absolute values, this can make the solution of the problem much easier than breaking the problem into different cases. can be interpreted as meaning that the distance between x and a is equal to b. For many more advanced problems involving absolute values, this can make the solution of the problem much easier than breaking the problem into different cases.
So in this problem, the inequality
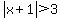
can be written as

and then this can be interpreted as "the distance between x and -1 is greater than 3".
This makes the solution simple. Thinking on a number line, 3 to the right of -1 is +2, so x can be any number greater than 2; and 3 to the left of -1 is -4, so x can be any number less than -4.
And again the solution set is  or or 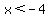 . .
|
|
|