SOLUTION: When a stopper is removed from the bottom of a barrel filled with water, the depth d, in centimeters, of a liquid in the barrel can be approximated by d=0.039t^2-5.816t+200, where

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: When a stopper is removed from the bottom of a barrel filled with water, the depth d, in centimeters, of a liquid in the barrel can be approximated by d=0.039t^2-5.816t+200, where       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1130410: When a stopper is removed from the bottom of a barrel filled with water, the depth d, in centimeters, of a liquid in the barrel can be approximated by d=0.039t^2-5.816t+200, where t is the time since stopper was removed from the hole. When will the depth be 125 cm? Round to the nearest tenth of a second.
So far I have:
125=0.039t^2-5.816t+200 then I subtracted 125 from both sides so the equation is equal to 0 which will make it 0=0.039t^2-5.816t+75 I know I need to factor it but I'm not sure how to go about that. Please help. Thank you.
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
When a stopper is removed from the bottom of a barrel filled with water, the depth d, in centimeters, of a liquid in the barrel can be approximated by d=0.039t^2-5.816t+200, where t is the time since stopper was removed from the hole. When will the depth be 125 cm? Round to the nearest tenth of a second.
So far I have:
125=0.039t^2-5.816t+200 then I subtracted 125 from both sides so the equation is equal to 0 which will make it 0=0.039t^2-5.816t+75 I know I need to factor it but I'm not sure how to go about that.
-------------
0.039t^2-5.816t+75 = 0
-----
It might be factorable, might not.
Use the quadratic equation:
---
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 0.039x%5E2%2B-5.816x%2B75+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-5.816%29%5E2-4%2A0.039%2A75=22.125856.

Discriminant d=22.125856 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--5.816%2B-sqrt%28+22.125856+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-5.816%29%2Bsqrt%28+22.125856+%29%29%2F2%5C0.039+=+134.869396428846
x%5B2%5D+=+%28-%28-5.816%29-sqrt%28+22.125856+%29%29%2F2%5C0.039+=+14.258808699359

Quadratic expression 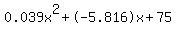0.039x%5E2%2B-5.816x%2B75 can be factored:
0.039x%5E2%2B-5.816x%2B75+=+%28x-134.869396428846%29%2A%28x-14.258808699359%29
Again, the answer is: 134.869396428846, 14.258808699359. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+0.039%2Ax%5E2%2B-5.816%2Ax%2B75+%29

It cannot be factored, but there's another problem.
It's a parabola that opens upward, giving 2 solutions for t.
Check your equation for d.