Question 113038: i need your help to solve this here it is
the attendance at a baseball game was 400 people. student tickets cost $2 and adult tickets cost $3.total ticket sales were $1050. how many tickets of each type were sold
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! To solve this one, you need to realize that you are dealing with two types of information. First is the number of tickets of each type, and second is the VALUE of each of the two types of tickets.
Step 1:
Let's call the number of student tickets S, and the number of adult tickets A.
Step 2:
Since we know that 400 people attended (which we have to presume means that 400 tickets were sold), we can write:
Step 3:
Since each student ticket costs $2, the total amount of money collected for all of the student tickets sold is 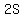 dollars. Similarly, the adult tickets account for  dollars worth of the $1050 total amount collected. Now we can write:
Step 4:
Solve this system of two linear equations in two unknowns. Since the first equation is rather simple with both variable having a coefficient of 1, I would choose the substitution method.
Step 5:
Find an expression for one of the variables. (Doesn't matter which, just pick one)
, so  . Now that we have an expression for S, we can substitute this expression into the second equation.
 .
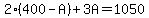Step 6:
Simplify and solve for A.
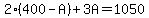
Step 7:
Substitute back to find the other variable. Now we know that there were 250 adult tickets sold, so we put that value back into the first equation:
And we have our answer. 150 student tickets and 250 adult tickets.
Last step -- VERY IMPORTANT. Check your answer.
 ...Check.
 ...Also check.
Now we are done.
Hope that helps.
John
|
|
|
