Question 1130147: Using proof by contradiction, show that (3+√2)/3 is irrational.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will assume that we accept  as irrational (proof provided at the end, for completeness): as irrational (proof provided at the end, for completeness):
Assume  where p,q are relatively prime integers, both greater than zero where p,q are relatively prime integers, both greater than zero

Write 3p as P, where P is obviously also an integer:

Re-arrange:

The RHS is integer minus integer, which must produce another integer (integers are closed under subtraction). Call it R:

 where R and q are integers, a contradiction. where R and q are integers, a contradiction.
Therefore, 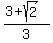 is irrational. is irrational.
——
Proof that  is irrational: is irrational:
 p,q relatively prime integers p,q relatively prime integers


LHS is even —> RHS must also be even, but this contradicts p,q being relatively prime. Thus  is irrational. is irrational.
|
|
|