SOLUTION: factor 5a^2-7ab-6b^2

Consider an equation

5a^2 - 7ab - 6b^2 = 0.       (1)



Divide both sides by b. You will get the equation

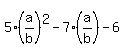 = 0.



Introduce new variable  x = .  Then the last equation takes the form

5x^2 - 7x - 6 = 0.    (2)



Find its roots using the quadratic formula

 =  =  = .


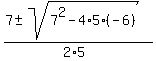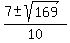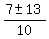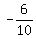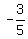So, the roots are   =   and  2.



It means that the polynomial (2) can be factored in this way

5x^2 - 7x - 6  = 5*(x-2)*(x+3/5) = (x-2)*(5x+3).



Returning to variables "a" and "b", you get

5a^2 - 7ab - 6b^2 = (a-2b)*(5a+3b).       ANSWER

    If you have difficulties factoring such a quadratic polynomial of 2 variables 
        (in other words, if you do not see the factoring formula immediately before your eyes in your mind)
     do the following (as I did in my solution)


        - reduce your quadratic polynomial of two variable to the quadratic polynomial of one new variable;

        - then find the roots of the reduced quadratic polynomial using the quadratic formula;

        - then factor the reduced quadratic polynomial using its roots;

        - then return back to the original variables "a" and "b".