SOLUTION: A transverse wave on a metal guitar string with a linear mass density of 2.3 g/m travels at 193.0 m/s. What is the tension on the string in N?

From your Physics textbook or from the Internet, you can learn that for an elastic string, velocity of the transverse wave is


    v = ,


where  "T"  is tension of the string (in Newtons, N)  and  "d" is the linear density of the string (in kilograms per meter, kg/m).


In this formula, the velocity "v" of the transverse wave is in meters per second, m/s.


By substituting the given input values, you get


    193 = .


Square both sides and express  T = 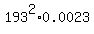  to get the value of  T  equal to  85.67 Newtons.


Answer.  The tension of the string is  85.67 Newtons.