SOLUTION: A block of mass 108.0 g sitting on a frictionless horizontal surface is attached to a spring with spring constant 28.0 N/m. Assume that the block is pulled from its equilibrium pos

The simplest way to solve the problem is to apply the Mechanical Energy conservation law.


The kinetic energy (when the body has its maximum speed - at the equilibrium position) is


    E = .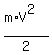


The potential energy (when the body is maximally far from the equilibrium) is


    P = ,


where "k" is the spring constant (given) and L is the maximum deviation from the equilibrium.


The conservation of energy law gives you  


    E = P,  which implies 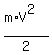  = ,   or


    L = .


Substitute the given data to determine L:


    L =  = 0.0205 m    (or 2.05 centimeters).


Maximal force is when the block is at the maximum deviation, and it is equal to


    F = k*L.


At the same time F = ma (Newton's second law), which gives you


    a = 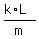 =  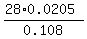= 5.315 .    ANSWER