Question 1130004: Solve the equation (y+5/y)^2 + 3(y+5/y)=4 ,using substitution u=y+5/y
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the equation (y+5/y)^2 + 3(y+5/y)=4 ,using substitution u=y+5/y
~~~~~~~~~~~~~~~~~~~~~
When you introduce new variable u = 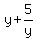 , the original equation takes the form
u^2 + 3u - 4 = 0.
Factoring, you get
(u+4)*(u-1) = 0,
which gives you two roots u= -4 and u= 1.
Thus, now you need to solve two equations , the original equation takes the form
u^2 + 3u - 4 = 0.
Factoring, you get
(u+4)*(u-1) = 0,
which gives you two roots u= -4 and u= 1.
Thus, now you need to solve two equations 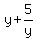 = -4 and = -4 and 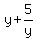 = 1 to find possible solutions for "y".
1) = 1 to find possible solutions for "y".
1) 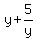 = -4 <====> is equivalent to = -4 <====> is equivalent to
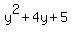 = 0 <=====> is equivalent to = 0 <=====> is equivalent to
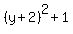 = 0 or = 0 or 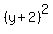 = -1
which has no solutions in real numbers,
but has two solutions in complex numbers x= -2 + i and x= -2 -i.
2) = -1
which has no solutions in real numbers,
but has two solutions in complex numbers x= -2 + i and x= -2 -i.
2) 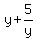 = 1 <====> is equivalent to = 1 <====> is equivalent to
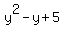 = 0 <=====> is equivalent to = 0 <=====> is equivalent to
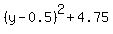 = 0 or = 0 or 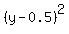 = -4.75,
which has no solutions in real numbers,
but has two solutions in complex numbers x= = -4.75,
which has no solutions in real numbers,
but has two solutions in complex numbers x= 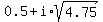 and x= and x= 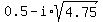 .
Answer. Your original equation has no solution/solutions in real numbers, but has 4 (four) solutions in complex numbers, listed above. .
Answer. Your original equation has no solution/solutions in real numbers, but has 4 (four) solutions in complex numbers, listed above.
Solved and explained.
|
|
|