SOLUTION: Find the sum of 1sin(1 degree)+2sin(2 degrees)+3sin(3 degrees)+4sin(4 degrees)+...+178sin(178 degrees)+179sin(179 degrees)+180sin(180 degrees).

Let  R = 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°).


It is even more convenient for me to write


    R = 0*sin(0°) + 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)  by adding  0*sin(0°) = 0  as the first term.


Then I can write


    R =   0*sin(0°)   + 1*sin(1°)     + 2*sin(2°)    + 3*sin(3°)     + . . . + 180*sin(180°)     (1)

    R = 180*sin(180°) + 179*sin(179°) + 178*sin178°) + 177*sin(177°) + . . . + 0*sin(0°).        (2)


Note that sin(0°) = sin(180°);  sin(1°) = sin(179°);  sin(2°) = sin(178°);  sin(3°) = sin(177°);  and so on.   
Therefore, adding  (1)  and  (2)


   2R = 180*(sin(0°) + sin(1°) + sin(2°) + sin(3°) + . . . + sin(90°)).


So, our sum R is the same as


     R = 90*(sin(0°) + sin(1°) + sin(2°) + sin(3°) + . . . + sin(90°)).


Now, let z = cos(1°) + i*sin(1°)  is this complex number.


Then, according to the de Moivre's formula


          = cos(2°) + i*sin(2°)

          = cos(3°) + i*sin(3°),

              .  .  .  .  .  .

           = cos(90° + i*sin(90°),

and the sum R  is 90 times the imaginary part  of the sum of the geometric progression

          Q = 1 +  +  +  +  + . . . + .


The sum of the geometric progression is  


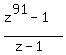     =  = now I will work to extract the imaginary part =  = 

  =  . 


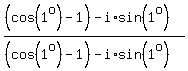So, the imaginary part has the DENOMINATOR  (cos(1°)-1)^2+sin^2(1°) = 2-2*cos(1°) = 2*(1-cos(1°)).


The imaginary part has the NUMERATOR  sin(91°)*(cos(1°)-1) - (cos(91°)-1)*sin(1°) = sin(91°)*cos(1°) - cos(91°)*sin(1°) - sin(91°) + sin(1°) = 

                                    = sin(90°) - sin(91°) + sin(1°) = 1 - cos(1°) + sin(1°).


Therefore, the answer is:  

    the sum  R = 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°) = .


You can transform it further as you want and/or as you need.


You can even get the numerical value, using your calculator.