Question 1129840: The perpendicular bisectors of sides
AC
and
BC
of ΔABC intersect side
AB
at points P and Q respectively, and intersect each other in the exterior (outside) of ΔABC. Find the measure of ∠ACB if m∠CPQ = 78° and m∠CQP = 62
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

Let  be the midpoint of side be the midpoint of side  , then by SAS similarity postulate, Δ , then by SAS similarity postulate, Δ 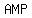 is congruent to Δ is congruent to Δ  . .
Thus,  < < 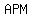 = =  < < 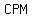
But  < <  + +  < < 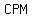 + +  < <  = =  ° °
⇒ 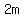 < < 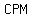 = =  ° °
⇒  < <  ° °
But  < < 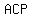 = =  ° - ° -  < < 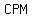 = =  °. °.
Similarly, let  be the midpoint of side be the midpoint of side  , then by , then by 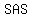 similarity postulate, Δ similarity postulate, Δ 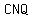 is congruent to Δ is congruent to Δ 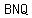 . .
Thus,  < <  = = < < 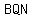
But,  < < 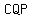 + +  < <  + +  < <  ° °
⇒ 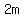 < < 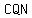 = =  ° °
⇒  < <  ° °
But,  < <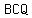 = =  - -  < < 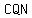 = =  ° °
 < < 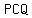 = =  ° - ° - < <  - -  < < 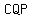 = =  ° °
Therefore,  < <  = =  < < 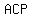 + +  < <  + +  < <  = =  ° °
so, your answer is:
 < <  = =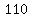 ° °
|
|
|