SOLUTION: I've been stuck trying to solve this. Could someone help explain how to correctly set up the equation. Thanks A scientist begins with 250 grams of a radioactive substance. After

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: I've been stuck trying to solve this. Could someone help explain how to correctly set up the equation. Thanks A scientist begins with 250 grams of a radioactive substance. After       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1129782: I've been stuck trying to solve this. Could someone help explain how to correctly set up the equation. Thanks
A scientist begins with 250 grams of a radioactive substance. After 250 minutes, the sample has decayed to 32 grams. Write an exponential equation
f(t) representing this situation. (Let f be the amount of radioactive substance in grams and t be the time in minutes.)
The exponential equation that I thought was correct, but isn't is 250* 2( -t/h).

Found 2 solutions by josmiceli, MathTherapy:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
Let +r+ = rate of decay in 250 min
When +t=250+ this is true:
+32+=+250%2A%28+1+-+r+%29%5E%28t%2F250%29+
+32+=+250%2A%28+1+-+r+%29%5E%28250%2F250%29+
+32+=+250%2A%28+1+-+r+%29+
+1+-+r+=+.128+
+r+=+.872+, so I can say:
+f%28t%29+=+250%2A%28+1+-+.872+%29%5E%28+t%2F250+%29+
-------------------------------------
check:
+f%28+250+%29+=+250%2A.128%5E%28250%2F250%29+
+f%28250%29+=+250%2A.128%5E1+
+f%28250%29+=+32+
OK
Feel free to get another opinion, too


Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
I've been stuck trying to solve this. Could someone help explain how to correctly set up the equation. Thanks
A scientist begins with 250 grams of a radioactive substance. After 250 minutes, the sample has decayed to 32 grams. Write an exponential equation
f(t) representing this situation. (Let f be the amount of radioactive substance in grams and t be the time in minutes.)
The exponential equation that I thought was correct, but isn't is 250* 2( -t/h). 
Exponential GROWTH rate formula: matrix%281%2C3%2C+y%2C+%22=%22%2C+A%5Bo%5Db%5Et%29, where:

y   = REMAINING amount of substance (32, in this case)

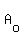A%5Bo%5D = INITIAL amount of substance (250 g, in this case)

b   = GROWTH rate of substance (Unknown, in this case)

t   = time substance takes to grow (250 minutes, in this case)

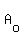matrix%281%2C3%2C+f%28x%29%2C+%22=%22%2C+A%5Bo%5Db%5Et%29

matrix%281%2C3%2C+32%2C+%22=%22%2C+250b%5E250%29 ------- Substituting 32 for f(x), or y, 250 for A%5Bo%5D, and 250 for t

matrix%281%2C3%2C+32%2F250%2C+%22=%22%2C+b%5E250%29

matrix%281%2C3%2C+16%2F125%2C+%22=%22%2C+b%5E250%29 ------- Reducing fraction on left

 ------- Multiplying both sides by the matrix%281%2C2%2C+%281%2F250%29%5Eth%2C+root%29



0.991810816, or .9918 = b

Exponential equation: highlight_green%28matrix%281%2C3%2C+f%28t%29%2C+%22=%22%2C+250%28.9918%29%5Et%29%29

Note: "b", being less than 1 (.9918) indicates a DECAY. If "b" were greater than 1, then that'd signify a GROWTH, as opposed to DECAY.



OR



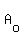As this is substance, which DECAYS/GROWS exponentially, the CONTINUOUS GROWTH/DECAY formula, or matrix%281%2C3%2C+A%2C+%22=%22%2C+A%5Bo%5De%5E%28kt%29%29 is used.

matrix%281%2C3%2C+32%2C+%22=%22%2C+250e%5E%28250k%29%29 -------- Substituting 32 for A, 250 for A%5Bo%5D, and 250 for t

matrix%281%2C3%2C+32%2F250%2C+%22=%22%2C+e%5E%28250k%29%29

matrix%281%2C3%2C+16%2F125%2C+%22=%22%2C+e%5E%28250k%29%29 ---------- Reducing fraction on left side

matrix%281%2C3%2C+250k%2C+%22=%22%2C+ln+%2816%2F125%29%29 -------- Converting to NATURAL LOGARITHMIC (ln) form

k, or rate of growth/decay = matrix%281%2C3%2C+ln+%2816%2F125%29%2F250%2C+%22=%22%2C+-+0.0082229%29

As k is negative (< 0), then the substance DECAYED as opposed to it GROWING. This we already know based on the fact that initially the substance was 250 g, and reduced to 32 g in  250 hours. 

However, it's good to know that when the CONTINUOUS GROWTH/DECAY formula is used, GROWTH is indicated by a POSITIVE (> 0) value for k, and DECAY, by a NEGATIVE (< 0) value for k.



The equation for CONTINUOUS GROWTH/DECAY of a substance, or: