Question 1129748: In a survey of 1000 person it was found that (1) 600 drink,(2) 720 smoke,(3) 560 chew,(4) 380 drink and smoke, (5)270 drink and chew,(6)350 smoke and chew,(7)80 drink, smoke and chew.what is the probability that a person is (a) do not drink or smoke (2) drink,smoke,but do not chew?
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem's formulation in the post is not precisely exact, so I reformulated it in this way:
In a survey of 1000 person it was found that (1) 600 drink,(2) 720 smoke,(3) 560 chew,
(4) 380 drink and smoke, (5)270 drink and chew,(6)350 smoke and chew,(7)80 drink, smoke and chew.
what is the probability that a person  is (a) do not drink or smoke (2) drink, smoke, but do not chew? is (a) do not drink or smoke (2) drink, smoke, but do not chew?
Solution
You have these subsets
(1) D, n(D) = 600;
(2) S, n(S) = 720;
(3) C, n(C) = 560;
(4) DS, n(DS) = 380;
(5) DC, n(DC) = 270;
(6) SC, n(SC) = 350;
(7) DSC, n(DSC) = 80. // All abbreviations are OBVIOUS and SELF-EXPLANATORY.
Then you can find
n(D U S U C) = n(D) + n(S) + n(C) - n(DS) - n(DC) - n(SC) + n(DSC) =
= 600 + 720 + 560 - 380 - 270 - 350 + 80 = 960.
It is the number of those who is ether D, or S, or C.
Hence, the number of those who is NEITHER D, NOR S, NOR C is 1000-960 = 40.
Now I am in position to answer the questions.
(a) Now, the number of those who do not drink or smoke is
n(D U S U C) - n(D) - n(S) + n(DS) + 40 = 960 - 600 - 720 + 380 + 40 = 60.
Hence, the probability (a) is  = =  = =  = 0.06 = 6%. ANSWER
(b) The number of those who D, S but not C is n(DS) - n(DSC) = 380 - 40 = 340,
and the probability (b) is = 0.06 = 6%. ANSWER
(b) The number of those who D, S but not C is n(DS) - n(DSC) = 380 - 40 = 340,
and the probability (b) is 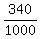 = =  = =  = 0.34 = 34%. ANSWER = 0.34 = 34%. ANSWER
Solved.
--------------
I just MANY TIMES explained in this forum on how to solve such problems.
If you need more explanations, or if you want to see other similar solved problems, look into my lessons
- Advanced problems on counting elements in sub-sets of a given finite set
- Challenging problems on counting elements in subsets of a given finite set
in this site and into my posts in this forum
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1129554.html
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1129554.html
https://www.algebra.com/algebra/homework/Rate-of-work-word-problems/Rate-of-work-word-problems.faq.question.1126097.html
https://www.algebra.com/algebra/homework/word/evaluation/Evaluation_Word_Problems.faq.question.1126099.html
H a p p y l e a r n i n g ! !
|
|
|