SOLUTION: at what time is your roller coaster at ground level with a polynomial value of x^5-4x^4-7x^3+14x^2-44x+120 and also the breakdown to the exact value of the roots

Algebra ->  Rational-functions -> SOLUTION: at what time is your roller coaster at ground level with a polynomial value of x^5-4x^4-7x^3+14x^2-44x+120 and also the breakdown to the exact value of the roots      Log On


   

Question 1129726: at what time is your roller coaster at ground level with a polynomial value of x^5-4x^4-7x^3+14x^2-44x+120 and also the breakdown to the exact value of the roots
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
breakdown to the exact value of the roots:
x%5E5-4x%5E4-7x%5E3%2B14x%5E2-44x%2B120+=0
x%5E5-2x%5E4-2x%5E4-11x%5E3%2B4x%5E3%2B22x%5E2-8x%5E2-60x%2B16x%2B120=0

x%5E4%28x-2%29-11x%5E2%28x-2%29-2x%5E3%28x-2%29-8x%28x-2%29-60%28x%2B2%29=0
%28x-2%29%28x%5E4-2x%5E3-11x%5E2-8x-60%29=0
%28x-2%29%28x%5E4-2x%5E3-15x%5E2%2B4x%5E2-8x-60%29=0
%28x-2%29%28%28x%5E4%2B4x%5E2%29-%282x%5E3%2B8x%29-%2815x%5E2%2B60%29%29=0
%28x-2%29%28x%5E2%28x%5E2%2B4%29-2x%28x%5E2%2B4%29-15%28x%5E2%2B4%29%29=0
%28x-2%29%28x%5E2+%2B+4%29%28x%5E2+-+2+x+-+15%29=0
%28x-2%29%28x%5E2+%2B+4%29%28x%5E2+-+5x%2B3x+-+15%29=0
%28x-2%29%28x%5E2+%2B+4%29%28%28x%5E2+-+5x%29%2B%283x+-+15%29%29=0
%28x-2%29%28x%5E2+%2B+4%29%28x%28x+-+5%29%2B3%28x+-+5%29%29=0
%28x+-+2%29+%28x+%2B+3%29+%28x+-+5%29+%28x%5E2+%2B+4%29=0

the coaster returns to ground level at x+=+2, x=5, x+=+-3, the three real zeros of the function



Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
at what time is your roller coaster at ground level with a polynomial value of x^5-4x^4-7x^3+14x^2-44x+120 and also the breakdown to the exact value of the roots
Using the RATIONAL ROOT THEOREM, find 2 zeroes. I found 2 zeroes to be 2 and - 3, which results in the 2 factors, (x - 2) and (x + 3). 

FOILing that gives you a trinomial that can be used as the DIVISOR, and with the LONG-DIVISION-of-POLYNOMIALS method, you get yet another trinomial (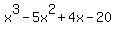x%5E3+-+5x%5E2+%2B+4x+-+20). 

Using the RATIONAL ROOT THEOREM again will result in a factor (x - 5), and along with LONG-DIVISION-of-POLYNOMIALS method, will result in a binomial (x%5E2+%2B+4), which

cannot be factored further.

We now get: 

Do you think you can continue from here?

OR

After finding ALL zeroes (there're 3 of them), use each and synthetic division to find the fourth and final factor, and from that, the final zero/solution.