Question 1129635: Give an example of a function, f(x), with a domain of (0,5] and a range of [0,∞)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! An example of a function, f(x), with a domain of ( , , ] and a range of [ ] and a range of [ , , ) is following: ) is following:
 when when 
to prove:
 , then , then 
 , then , then 
thus, function of  have a domain of ( have a domain of ( , , ] and a range of [ ] and a range of [ , , ) )
another example:
The domain is ( , , ], which includes all real numbers between ], which includes all real numbers between  and and  , excluding , excluding  and including and including  . .
The functions that do not have  in its domain are for example: in its domain are for example:  . .
The domain of  is all the real numbers except is all the real numbers except  ,i.e., ( ,i.e., ( , , ) U ( ) U ( , , ). ).
To find a way to 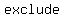 the negative numbers from the domain is by remembering that the the negative numbers from the domain is by remembering that the 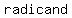 of a square root of a square root  be be 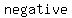 . .
So having that in mind, and applying that to the example above gives the following result:  , and its domain is ( , and its domain is ( , , ). ).
The domain also  include include  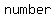 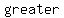 than than  , therefore , therefore 
This function requires  (for the top) and (for the top) and 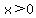 (for the bottom). (for the bottom).
So the domain of  is ( is ( , , ]. ].
Now about the 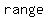 : square roots are : square roots are 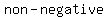 , so , so    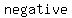 . .
When  , ,  , which is the smallest value of , which is the smallest value of  . .
On can note that  gets closer and closer to gets closer and closer to  , the numerator gets closer and closer to , the numerator gets closer and closer to  , and the , and the  gets even to gets even to 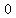 (still being (still being 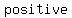 ). ).
Since 
the square root function is an increasing function, we can just consider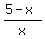
As the denominator gets smaller, the expression 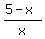 gets bigger. gets bigger.
So, the function  satisfies the requirement of the posted question. satisfies the requirement of the posted question.
|
|
|