Question 1129579: Sec. 12.3 # 48
23. Quartiles The prices of the 20 top-rated top-loading washing machines, as reported in the August, 2014, issue of Consumer Reports, are as follows:
$1200$950$1100$600$750$800$800$1000$1000$1200$800$700$900$1000$700$1500$1000$1000$800$700$1200$950$1100$600$750$800$800$1000$1000$1200$800$700$900$1000$700$1500$1000$1000$800$700
23. Determine
a. Q2
b. Q1
c. Q3
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! your data in order from lowest to highest:
 ,, ,,,,,, ,, ,,,,,,,, ,,
 ,, ,,,,,,,,
,, ,, ,,,, ,
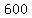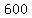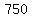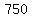The first quartile (or lower quartile or  th percentile) is the median of the bottom half of the numbers. So, to find the first quartile, we need to place the numbers in value order and find the bottom half.
So, the bottom half is
,,,,,,,,,,,,,,,,,,,
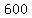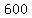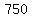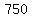The median of these numbers is  .
The third quartile (or upper quartile or 75th percentile) is the median of the upper half of the numbers. So, to find the third quartile, we need to place the numbers in value order and find the upper half.
So, the upper half is
,,,,,,,,,,
,,,,,,,,,
The median of these numbers is  .
The median (also written as  ) is the middle number in a sorted list of numbers. So, to find the median, we need to place the numbers in value order and find the middle number.
Ordering the data from least to greatest, we get:
,,,,,,,,,,,,,,,,,,, , ,,,,,,,,,,,,,,,,,,,
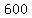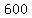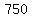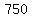As you can see, we do not have just one middle number but we have a pair of middle numbers, so the median is the average of these two numbers:
a.
b. 
c.
|
|
|
