Question 1129281: If k is multiple of 24 not but a multiple of 16. Which of the following cannot be an integer?
Found 3 solutions by MathLover1, MathTherapy, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If  is a multiple of is a multiple of  , then , then  contains all of contains all of  ís primes. All you know thus far is that it contains ís primes. All you know thus far is that it contains   ís and a ís and a  . .
You also know that it is  a multiple of a multiple of  . That means that it doesnít contain the primes of . That means that it doesnít contain the primes of  , which are , which are   's. 's.
That is, there are already   ís in there, and there ís in there, and there   be be  more. If there were, then more. If there were, then  would be divisible by would be divisible by  . .
In summary:
 contains exactly contains exactly   ís, at ís, at  one one  , and possibly some other primes you donít know about. , and possibly some other primes you donít know about.
If thatís the case, what numbers could divide evenly into ? ?
we know   ís make ís make 
 divides evenly into divides evenly into  , since there are , since there are   ís in ís in  =>this =>this 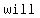  an integer an integer
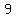 could divide evenly into could divide evenly into , since there , since there 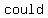  two two  ís in ís in =>this =>this 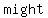 be an integer be an integer
 canít divide evenly into canít divide evenly into  , there are , there are   ís in ís in  , but there is , but there is  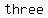  ís in ís in 
so,  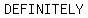 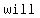   an integer; consequently, this is the right an integer; consequently, this is the right 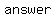
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When you pronounciate "Which of the following . . . ", it assumes that you then LIST that follows - otherwise
your post becomes non-sensical.
|
|
|