Question 1129273: Find the discriminant as a function of k, and hence find the values of k for which 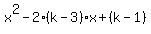 is positive definite.
Please explain the reasoning behind > and <, as they don't seem to follow conventional rules when using a discriminant.
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! Let ax^2 +bx +c = 0 be a quadratic equation, then
:
Discriminant(D) = b^2 -4ac
:
given f(x) = x^2 -2(k-3)x +(k-1) is positive definite
:
D = (-2k+6)^2 -4(1)(k-1)
:
f(x) is a parabola, since a>0, f(x) is definite, that is, f(x) does not cross the x axis
:
Note f(x) is definite if D < 0
:
f(x) is positive if a > 0, that is, f(x) opens upward, therefore
:
f(x) is positive definite if it opensto summarize upward and does not cross the x-axis
:
(-2k+6)^2 -4(1)(k-1) < 0
:
4k^2 -24k +36 -4k +4 < 0
:
k^2 -6k +9 -k +1 < 0
:
k^2 -7k +10 < 0
:
(k-5)(k-2) < 0
:
therefore k belongs to the open interval (2, 5)
:
Note if D > o, then f(x) crosses the x axis and f(x) is called indefinite
:
|
|
|
